$1 公共基础知识
Q1. 二叉树相关计算
Q1-1.在深度为7的满二叉树中,叶子结点的总个数是?答案:C
A.32 B.31 C.64 D.61
其中 ( k ) 是树的深度,对于深度为7的满二叉树,( k = 7 )。所以:深度为7的满二叉树中叶子节点的总个数是64个。
Q1-2.某二叉树有49个度为2的结点,4个度为1的结点,则答案:A
A、该二叉树共有103个结点
B、该二叉树的结点数不确定
C、该二叉树共有101个结点
D、不可能有这样的二叉树
Q2. 数据模型相关
Q2-1. 树形结构表示实体之间联系的模型是
答案:层次模型Q2-2. 辑模型是面向数据库系统的模型,下面属于逻辑模型的是答案:C。
A.谓词模型
B.物理模型
C.关系模型
D.实体-联系模型
逻辑数据模型又称为数据模型,是面向数据库系统的模型,着重于在数据库系统一级的实现。成熟并大量使用的逻辑模型有层次模型、网状模型、关系模型和面向对象模型等。
Q3. 软件工程相关
Q3-1.软件工程包含哪三个要素?答案:方法、工具、过程
Q3-2.需求分析阶段产生的主要文档是?答案:A
A.数据流图和数据字典
B.初步的用户手册
C.需求规格说明书
D.确认测试计划
Q4. 计算机基础部分
Q4-1.关于冯·诺依曼计算机结构描述正确的是?答案:A
A. 存储程序控制的计算机结构
B. 需求驱动的归约计算机结构
C. 模式匹配驱动的智能计算机结构
D. 数据驱动的数据流计算机结构
"存储程序”思想是冯·诺依曼等人在1946年6月首先提出来的,它可以简要地概括为以下几点:
①计算机(指硬件)由运算器、控制器、存储器、输入设备和输出设备五大基本部件组成;
②计算机内部用二进制来表示指令和数据;
③需将编好的程序和原始数据事先存入存储器中,然后再启动计算机工作。本题答案为A选项。本题选择A选项。
Q4-2. I/O方式中的程序查询方式是指答案:A
A.在程序执行前系统首先检查该程序运行中所需要的I/O设备是否准备
B.当CPU需要执行I/O操作时,程序将主动查询I/O设备是否准备好
C.用程序检查系统中I/O设备的好坏
D.用程序启动I/O设备
程序查询方式是指程序主动查询输入输出设备是否准备好:如果准备好,CPU执行/O操作:否则,CPIU会一直查询并等待设备准备好后执行I/O操作。
Q4-3. 一进程已获得除CPU以外的所有所需运行资源,经调度分配CPU给它后,该进程将进入答案:A
A.运行状态
B.就绪状态
C.活动状态
D.阻塞状态
一个进程的活动情况至少可以划分为以下5种基本状态:
(1)运行状态处于运行状态的进程实际上正占据着CPU。显然,处于这种状态的进程数目不能多于CPU的数目。在单CPU的情况下,处于运行状态的进程只能有一个。
(2)就绪状态这种状态下的进程已获得除CPU以外的一切所需资源,只是因为缺少CPU而不能运行,一旦获得CPU,它就立即投入运行。
(3)等待状态一个进程正在等待某一事件的发生而暂时停止执行。在这种状态下,即使把CPU分配给它,该进程也不能运行,即处于等待状态,又称为阻塞状态或封锁状态。(4)创建状态进程正在创建过程中,尚不能执行。
(5)终止状态进程运行结束。
Q5. 数据结构与算法
二叉树题目参考:2021年12月/2022年3月计算机二级公共基础知识押题51-60 - 知乎 (zhihu.com)
Q5-1. 设栈与队列初始状态为空。将元素A, B, C, D, E, F, G, H依次轮流入栈和入队, 然后依次轮流退队和出栈, 则输出序列为答案:B
〖A〗G, B, E, D, C, F, A, H
〖B〗B, G, D, E, F, C, H, A
〖C〗D, C, B, A, E, F, G, H
〖D〗A, B, C, D, H, G, F, E
栈是先进后出的线性表, 队列是先进先出的线性表。
将元素A, B, C, D, E, F, G, H依次轮流入栈和入队, 这时栈中的元素为ACEG, 队列中的元素为BDFH; 然后依次轮流退队和出栈, 即队列中B元素退队, 然后栈中G元素出栈, 队列中D元素退队, 栈中E元素出栈, 以此顺序, 完成所有元素退队和出栈, 则输出序列为B, G, D, E, F, C, H, A。
Q5-2. 树的度为3, 共有29个结点, 但没有度为1和2的结点。则该树中叶子结点数为答案:D
〖A〗0
〖B〗9
〖C〗18
〖D〗不可能有这样的树
树的度为3, 即树中只存在度为 0、1、2、3 的结点, 假设叶子结点数为 n , 由于没有度为 1 和 2 的结点, 则度为3的结点数为 $29 - n$ , 根据树中的结点数=树中所有结点的度之和 +1, 得 $3×(29 - n) + 0×1 + 0×2 + n×0 + 1 = 29$ , 得出的n不为整数, 因此不存在这样的树。
Q5-3. 循环队列的存储空间为Q(0 : 59), 初始状态为空。经过一系列正常的入队与退队操作后, front = 25, rear = 24。循环队列中的元素个数为?答案:C
〖A〗1
〖B〗2
〖C〗59
〖D〗60
设循环队列的存储空间为 $Q(1 : m)$ , 初始状态为空。
在循环队列运转起来后, 如果 $rear - front > 0$ , 则队列中的元素个数为 $rear - front$ 个; 如果 $rear - front < 0$ , 则队列中的元素个数为 $rear - front + m$ 。
本题中 $front = 25, rear = 24, rear - front < 0$ , 则元素个数为 $24 - 25 + 60 = 59$ 。
Q5-4. 某完全二叉树共有256个结点,则该完全二叉树的深度为?答案:C
〖A〗7
〖B〗8
〖C〗9
〖D〗10
根据完全二叉树的性质:具有 $n$ 个结点的完全二叉树的深度为 $[log₂n]+1$。本题中完全二叉树共有 256 个结点,则深度为 $[log₂256]+1=8+1=9$ 。
Q5-5. 现有表示患者和医疗的关系如下:P(P#,Pn,Pg,By),其中P#为患者编号,Pn为患者姓名,Pa为性别,Bv为出生日期,Tr(P#,D#,Date.Rt),其中D#为医生编号,Date为就诊日期,Rt为诊断结果。检索在1号医生处就诊的病人姓名的表达式是答案:A
A. TPn(TP#(D#=1(Tr)P)
B.TTP#(CD#=1(Tr)
C. TPn(P)
D. TTpn(TrDP)
关系代数中T表示投影运算,其下标表示需要投影出来的列;0表示选择运算,其下标表示选择过程中需要满足的条件;A表示并运算;>表示自然连接。首先在Tr表中找出在1号医生处就诊的记录OD#=1(Tr),并检索出这些记录中患者的编号TTp#(OD#=1(Tr)),检索结果与表P进行自然连接生成中间表TTo#(OD#=1(Tr))P,最后在中间表中检索患者的姓名Pn。故本题答案为A。
Q5-6.设表的长度为 n。下列查找算法中,在最坏情况下,比较次数最少的是?答案:A
A) 有序表的二分查找
B) 顺序查找
C) 寻找最大项
D) 寻找最小项
顺序查找和寻找最大项、最小项在最坏情况下比较次数为 n。对于长度为 n 的有
序线性表,在最坏情况下,二分法查找只需要比较 (log以2为底n为对数) 次。
Q5-7.列排序方法中,最坏情况下时间复杂度(即比较次数)最低的是?答案:A
A.希尔排序
B.快速排序
C.简单插入排序
D.冒泡排序
(1) 冒泡排序的总时间复杂度为 $O(n^2)$。这是因为在最坏的情况下,需要进行 $n-1$ 次遍历,每次遍历需要进行的比较次数从 $n-1$ 逐渐减少到 $1$。所以总的比较次数是 $\frac{n(n-1)}{2}$,这是一个等差数列求和公式。由于冒泡排序在每次遍历中还需要进行元素交换,所以时间复杂度是 $O(n^2)$。
(2) 快速排序的平均时间复杂度是 $O(n \log n)$,但在最坏的情况下,如果初始序列已经是有序的,快速排序的时间复杂度会退化到 $O(n^2)$。这是因为每次划分都会产生一个不平衡的划分,导致递归树的深度接近 $n$,从而使得比较和交换操作的次数接近于线性序列的平方。
(3) 希尔排序的时间复杂度与所选用的间隔序列有关,不同的间隔序列会导致不同的性能。在最坏的情况下,希尔排序的时间复杂度可能达到 $O(n^2)$,但通常情况下,它的表现会比这个要好。希尔排序的平均时间复杂度通常认为是 $O(n \log^2 n)$ 或 $O(n^{4/3})$,这取决于间隔序列的选择。
(4) 简单插入排序在最坏情况下的时间复杂度也是 $O(n^2)$。这是因为在最坏的情况下,序列是完全逆序的,每次插入操作都需要比较 $n-1, n-2, \ldots, 1$ 次,总共需要进行 $\frac{n(n-1)}{2}$ 次比较。
$3 Python 选择题部分
Q1-1.关于 Python 函数定义的参数设置,错误
的选项是答案:AA. def vfunc(*a, b):
B. def vfunc(a, *b):
C. def vfunc(a, b):
D. def vfunc(a, b=2):
Q1-2.变量s='shehuizhili,表达式s[-5:-1]的结果是? 答案:A
A.zhil
B.zhili
C.izhi
D.izhil
$3 Python 简单应用题
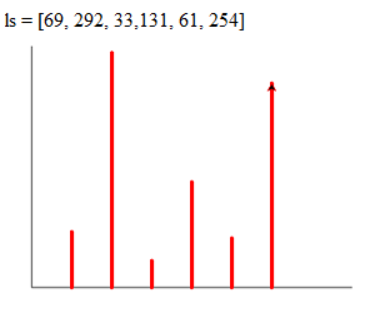
Q1. 根据列表中保存的数据采用 turtle 库画图直方图,显示输出在屏幕上,效果如下图所示。
在____________上补充代码
请不要修改其他代码
①
ls = [69, 292, 33, 131, 61, 254]
X_len = 400
Y_len = 300
x0 = -200
y0 = -100
t.penup()
t.goto(x0, y0)
t.pendown()
t.fd(X_len)
t.fd(-X_len)
t.seth(②)
t.fd(Y_len)
t.pencolor('red')
t.pensize(5)
for i in range(len(ls)):
t.③
t.goto(x0 + (i+1)*50,④)
t.seth(90)
⑤
t.fd(⑥)
t.done()#
# 在____________上补充代码
# 请不要修改其他代码
#
import turtle as t #更简洁地调用turtle库
ls = [69, 292, 33, 131, 61, 254]
X_len = 400
Y_len = 300
x0 = -200
y0 = -100
t.penup()
t.goto(x0, y0)
t.pendown()
t.fd(X_len)
t.fd(-X_len)
t.seth(90) #设置笔的起始角度
t.fd(Y_len)
t.pencolor('red')
t.pensize(5)
for i in range(len(ls)):
t.penup() #提起画笔
t.goto(x0 + (i+1)*50, y0) #移到绝对坐标处,这里x坐标动,y坐标不动
t.seth(90)
t.pendown() #放下画笔
t.fd(ls[i]) #表示直线爬行的距离
t.done()在已定义好的字典 pdict 里有一些人名及其电话号码。请用户输入一个人的姓名,在字典中查找该用户的信息,如果找到,生成一个四位数字的验证码,并将名字、电话号码和验证码输出在屏幕上,如示例所示。如果查找不到该用户信息,则显示“对不起,您输入的用户信息不存在。”示例如下:
输入:
Bob
输出:
Bob 234567891 1926
输入:bob
输出:
对不起,您输入的用户信息不存在。
#
# 在......上补充一行或多行代码
# 不得修改其他代码
#
import random
random.seed(2)
pdict= {'Alice':['123456789'],
'Bob':['234567891'],
'Lily':['345678912'],
'Jane':['456789123']}
name = input('请输入一个人名:')
if name in pdict:
print("①".format(②)
else:
print("对不起,您输入的用户信息不存在。")#
# 在......上补充一行或多行代码
# 不得修改其他代码
#
import random
random.seed(2)
pdict= {'Alice':['123456789'],
'Bob':['234567891'],
'Lily':['345678912'],
'Jane':['456789123']}
name = input('请输入一个人名:')
if name in pdict:
print("{} {} {}".format(name,pdict.get(name)[0],random.randint(1000,9999)))
else:
print("对不起,您输入的用户信息不存在。")